Μη-Sinusoidal Waveforms: τετράγωνες, ορθογώνιες και παλμικές κυματομορφές
Στην ηλεκτρονική μηχανική, η δημιουργία και διαμόρφωση ηλεκτρικών κυματομορφών είναι σημαντικά καθήκοντα που χρησιμοποιούνται σε πολλούς τομείς, συμπεριλαμβανομένων των συστημάτων επικοινωνίας και των ψηφιακών ηλεκτρονικών.Αυτό το άρθρο συζητούν τρεις τύπους κυματομορφών: τετραγωνικά κύματα, ορθογώνια κύματα και παλμικά κύματα, το καθένα με μοναδικά χαρακτηριστικά και χρήσεις.Τα τετράγωνα κύματα συμμετρία και γρήγορες μεταβάσεις μεταξύ των καταστάσεων είναι αυτό που τα καθιστούν τόσο αποτελεσματικά στην αλλαγή των εφαρμογών.Η ευελιξία των ορθογώνιων κυμάτων είναι χρήσιμη σε εργασίες όπως η διαμόρφωση πλάτους παλμού (PWM) και η επεξεργασία σήματος, όπου απαιτείται η ρύθμιση της κυματομορφής.Τα παλμικά κύματα είναι ακανόνιστα και μη επαναλαμβανόμενα, κατασκευασμένα για καταστάσεις όπου οι αλλαγές χρονισμού χρησιμοποιούνται για την αποστολή πληροφοριών.Αυτό το άρθρο διερευνά τα φυσικά χαρακτηριστικά αυτών των κυματομορφών, τον τρόπο με τον οποίο συμπεριφέρονται στην ανάλυση Fourier και τις πρακτικές χρήσεις τους.Η κατανόηση αυτών των λεπτομερειών βοηθά να επισημανθεί αυτό που καθορίζει κάθε κυματομορφή σε ηλεκτρονικές εφαρμογές.Εξετάζει επίσης τον τρόπο δημιουργίας κάθε κυματομορφής και τις κοινές χρήσεις για κάθε μία, παρέχοντας μια σαφέστερη εικόνα του τρόπου με τον οποίο συμβάλλουν στη βελτίωση των ηλεκτρονικών σχεδίων.
Κατάλογος
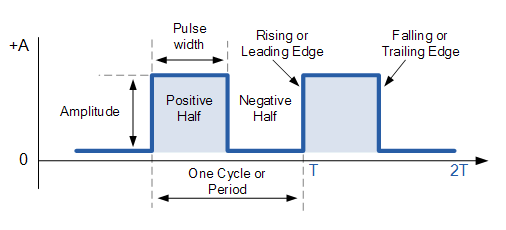
Εικόνα 1: τετραγωνική κυματομορφή
Χαρακτηριστικά τετραγωνικών κυμάτων
Τα τετράγωνα κύματα είναι κυματομορφές που μετακινούνται γρήγορα μεταξύ δύο επιπέδων τάσης που ονομάζονται "υψηλά" και "χαμηλά".Αυτές οι αλλαγές συμβαίνουν αμέσως, δημιουργώντας μια απότομη μετατόπιση μεταξύ των δύο καταστάσεων.Ωστόσο, σε πραγματικά συστήματα, παράγοντες όπως οι ιδιότητες κυκλώματος επιβραδύνουν τις μεταβάσεις.Ο χρόνος που χρειάζεται για την άνοδο ή την πτώση της τάσης καλείται χρόνος άνοδας (για ανερχόμενη) και πτώση (για να κατεβείτε).Ένα τέλειο τετράγωνο κύμα ξοδεύει ίσο χρόνο στις υψηλές και χαμηλές καταστάσεις, δημιουργώντας μια ισορροπημένη κυματομορφή.
Ο χρόνος που αφιερώνεται στις υψηλές και χαμηλές καταστάσεις μπορεί να διαφέρει, αλλά το κύμα εξακολουθεί να θεωρείται τετραγωνικό κύμα.Η αλλαγή αυτής της ισορροπίας μπορεί να είναι χρήσιμη για διαφορετικές εργασίες.Ωστόσο, όταν η ακρίβεια χρονισμού όπως στα συστήματα επικοινωνίας, είναι σημαντικό να διατηρηθεί η συμμετρία.Σε αυτές τις περιπτώσεις ενδέχεται να απαιτηθούν επιπλέον προσαρμογές σχεδιασμού.
Χαρακτηριστικά ορθογώνιων κυμάτων
Τα ορθογώνια κύματα είναι παρόμοια με τα τετράγωνα κύματα, αλλά έχουν ανομοιογενή υψηλά και χαμηλά φάσεις, δίνοντάς τους μεγαλύτερη ευελιξία.Ενώ τα τετράγωνα κύματα έχουν ίσο υψηλό και χαμηλό χρόνο, τα ορθογώνια κύματα σας επιτρέπουν να προσαρμόσετε αυτές τις φορές ξεχωριστά.Αυτό καθιστά τα ορθογώνια κύματα πιο χρήσιμα για καταστάσεις όπου δεν απαιτείται το αυστηρό πρότυπο τετραγωνικών κυμάτων.
Ένα μεγάλο πλεονέκτημα των ορθογώνιων κυμάτων είναι η ευελιξία τους.Με τη ρύθμιση των υψηλών και χαμηλών χρόνων, το πλάτος κάθε παλμού μπορεί να ελεγχθεί που είναι σημαντικό σε διαμόρφωση πλάτους παλμού (PWM).Το PWM χρησιμοποιείται σε πράγματα όπως ο έλεγχος του κινητήρα, τα συστήματα επικοινωνίας και ισχύος, όπου ο χρονισμός πρέπει να είναι ακριβής.Τα ορθογώνια κύματα είναι επίσης μεγάλα στην επεξεργασία και το χρονοδιάγραμμα σήματος.Για παράδειγμα, στα ψηφιακά ηλεκτρονικά, τα ορθογώνια κύματα μπορούν να χρησιμοποιηθούν ως σήματα ρολογιού με ρυθμιζόμενους χρονοδιαγράμματα για να βοηθήσουν στον συντονισμό διαφορετικών τμημάτων ενός συστήματος.Τα ορθογώνια κύματα είναι πιο ευέλικτα από τα τετραγωνικά κύματα, επειδή ο κύκλος λειτουργίας τους μπορεί να ρυθμιστεί.
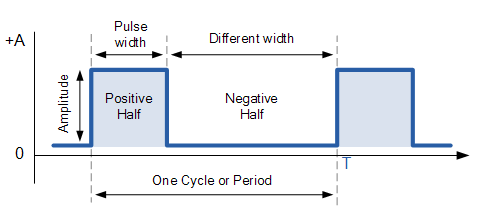
Εικόνα 2: ορθογώνια κυματομορφή
Χαρακτηριστικά των παλμικών κυμάτων
Οι παλμικές κυματομορφές είναι διαφορετικές από τις περιοδικές κυματομορφές επειδή δεν έχουν κανονικό, επαναλαμβανόμενο μοτίβο.Οι περιοδικές κυματομορφές επαναλαμβάνονται σε έναν σταθερό κύκλο, αλλά οι παλμικές κυματομορφές συμβαίνουν σε αντίδραση σε κάτι σαν να φτάσετε σε μια συγκεκριμένη τάση.Εξαιτίας αυτού, οι παλμικές κυματομορφές μπορούν να φαίνονται διαφορετικές ανάλογα με την κατάσταση.
Ένα σημαντικό πράγμα για τις παλμικές κυματομορφές είναι ότι μπορούν να φέρουν πληροφορίες αλλάζοντας το σχήμα και το χρονοδιάγραμμα.Οι περιοδικές κυματομορφές είναι πιο προβλέψιμες, αλλά οι παλμικές κυματομορφές μπορούν να ρυθμιστούν σε πραγματικό χρόνο για να παρουσιάσουν διαφορετικά είδη δεδομένων.Δεδομένου ότι οι παλμικές κυματομορφές μπορούν να αλλάξουν με βάση διαφορετικές συνθήκες, είναι ένα καλό εργαλείο για τη διαχείριση σύνθετων πληροφοριών.Η ικανότητά τους να προσαρμοστούν γρήγορα τους καθιστά σημαντικές για τις τεχνολογίες που χρειάζονται γρήγορες απαντήσεις και ευελιξία.
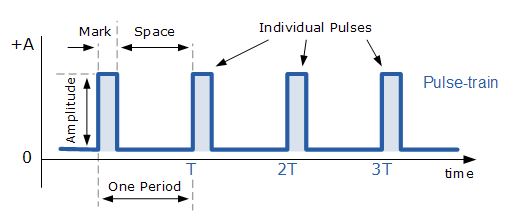
Εικόνα 3: Κυματομορφή παλμών
Ήχος τετραγωνικών, ορθογώνιων και παλμικών κυμάτων
Square Waves: Τα τετράγωνα κύματα έχουν έναν τολμηρό, αιχμηρό ήχο που ξεχωρίζει.Δημιουργούν αυτόν τον ισχυρό ήχο επειδή έχουν πολλές περίεργες αρμονικές, δίνοντάς τους ένα buzzy τόνο.Το κύμα μεταβαίνει γρήγορα μεταξύ υψηλών και χαμηλών επιπέδων που καθιστούν τον ήχο του "έντονο" και ικανό να κόψει άλλους ήχους σε ένα μίγμα.Τα τετράγωνα κύματα χρησιμοποιούνται σε ηλεκτρονική μουσική και synths, επειδή μπορούν να κάνουν τόσο βαθιά μπάσα όσο και αιχμηρά, προσελκύουν οδηγούς.
Ορθογώνια κύματα: Τα ορθογώνια κύματα είναι πιο ευέλικτα από τα τετράγωνα κύματα επειδή μπορείτε να αλλάξετε τον τόνο τους προσαρμόζοντας πόσο καιρό παραμένουν στη θέση "υψηλής".Όταν ο χρόνος που ξοδεύεται είναι περίπου το ήμισυ, ακούγονται σαν τετράγωνα κύματα με φωτεινό και πλούσιο τόνο.Αλλά αν ο χρόνος στο υψηλό κράτος γίνει μικρότερος, ο ήχος γίνεται λεπτότερος και πιο ρινικός.Αυτή η ευελιξία επιτρέπει στα ορθογώνια κύματα να δημιουργούν ένα ευρύ φάσμα ήχων από ισχυρό και έντονο στο φως και κοίλο.
Pulsed Waves: Τα παλμικά κύματα έχουν ένα γρήγορο, απότομο ήχο, καθιστώντας τα ιδανικά για ρυθμικά ή μικρά, κρουστά αποτελέσματα.Είναι καλοί στη δημιουργία γρήγορων εκρήξεων ήχου σαν κλικ ή μπιπ και να λειτουργούν καλά στη μουσική που χρειάζεται ισχυρά, ρυθμικά στοιχεία.Η γρήγορη άνοδος και πτώση των παλμικών κυμάτων τους δίνει μια επιθετική αίσθηση, έτσι χρησιμοποιούνται συχνά για συνθετικές μαχαιρίες.
Ανάλυση Fourier των τετραγωνικών, ορθογώνιων και παλμικών κυμάτων
Τετραγωνικά κύματα
Ένα τετράγωνο κύμα είναι μια κυματομορφή που μεταβαίνει γρήγορα μεταξύ μιας υψηλής και χαμηλής τιμής, ξοδεύοντας ίσο χρόνο σε κάθε επίπεδο.Χρησιμοποιώντας τη σειρά Fourier, μπορούμε να το εκφράσουμε ως άθροισμα ημιτονοειδών κυμάτων.Για ένα τετράγωνο κύμα με πλάτος Α και περίοδο t, η σειρά Fourier είναι:
![]()
Εδώ, το n αντιπροσωπεύει μόνο τους περίεργους ακέραιους, και ![]() είναι η συχνότητα του κύματος.Η σειρά ξεκινά με τη συχνότητα (πότε
είναι η συχνότητα του κύματος.Η σειρά ξεκινά με τη συχνότητα (πότε ![]() ) και περιλαμβάνει υψηλότερες περίεργες αρμονικές.Κάθε διαδοχική αρμονική μειώνεται στο πλάτος, ακολουθώντας το αντίστροφο του αρμονικού αριθμού.
) και περιλαμβάνει υψηλότερες περίεργες αρμονικές.Κάθε διαδοχική αρμονική μειώνεται στο πλάτος, ακολουθώντας το αντίστροφο του αρμονικού αριθμού.
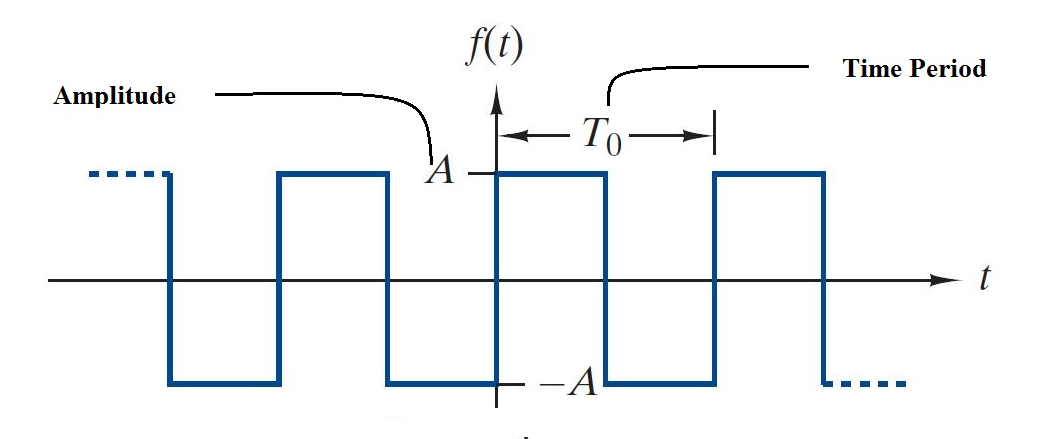
Εικόνα 4: τετράγωνα κύματα σε σειρά Fourier
Ορθογώνια κύματα
Τα ορθογώνια κύματα είναι παρόμοια με τα τετραγωνικά κύματα, αλλά ο χρόνος που αφιερώνεται στις υψηλές και χαμηλές καταστάσεις είναι άνισος.Σε αυτή την περίπτωση, η σειρά Fourier πρέπει να αντιπροσωπεύει τον "κύκλο λειτουργίας" d, το οποίο είναι το κλάσμα της περιόδου που το κύμα παραμένει στην υψηλή κατάσταση.Η σειρά Fourier για ένα ορθογώνιο κύμα είναι:
![]()
Αυτός ο τύπος προσαρμόζεται για τα διαφορετικά μήκη των υψηλών και χαμηλών καταστάσεων, ενσωματώνοντας τον κύκλο λειτουργίας D στα εξαρτήματα ημιτονοειδούς κύματος.
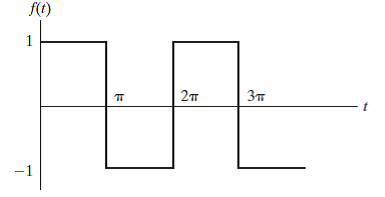
Εικόνα 5: ορθογώνια κύματα σε σειρά Fourier
Παλμικά κύματα
Τα παλμικά κύματα ή τα παλμικά τρένα αποτελούνται από επαναλαμβανόμενους παλμούς που χωρίζονται από διαστήματα όπου το σήμα είναι μηδέν.Η ανάλυση Fourier των αμαξοστοιχιών είναι πιο περίπλοκη επειδή εξαρτάται από το σχήμα των παλμών και το χρονοδιάγραμμα μεταξύ τους.Μια κοινή σειρά Fourier για ένα τρένο ορθογώνιων παλμών μοιάζει με:
![]()
Σε αυτή την έκφραση, το δ είναι το πλάτος κάθε παλμού, t είναι η περίοδος μεταξύ των παλμών, ![]() είναι η βασική συχνότητα του παλμού.Ο
είναι η βασική συχνότητα του παλμού.Ο ![]() λειτουργία, που ορίζεται ως
λειτουργία, που ορίζεται ως ![]() , περιγράφει τον τρόπο με τον οποίο το σχήμα του παλμού επηρεάζει τα εξαρτήματα συχνότητας.
, περιγράφει τον τρόπο με τον οποίο το σχήμα του παλμού επηρεάζει τα εξαρτήματα συχνότητας.
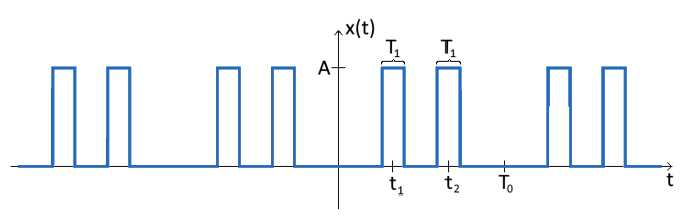
Εικόνα 6: Ανάλυση Fourier των αμαξοστοιχιών Pulse
Παραδείγματα ηλεκτρικών κυματομορφών
Τετραγωνικό κύμα
Ένα τετράγωνο κύμα είναι ένας από τους απλούστερους τύπους κυματομορφών.Εναλλάσσεται μεταξύ δύο επιπέδων, υψηλών και χαμηλών δαπανών ίσου χρόνου σε κάθε κράτος.Αυτή η ίση διαίρεση ονομάζεται κύκλος λειτουργίας 50%.
Εδώ σημαίνει αυτό:
• Το κύμα παραμένει "σε" για ένα συγκεκριμένο χρονικό διάστημα (υψηλό επίπεδο).
• Στη συνέχεια παραμένει "off" για ίσο χρονικό διάστημα (χαμηλό επίπεδο).
Για παράδειγμα, εάν το πλάτος παλμού είναι 10 χιλιοστά του δευτερολέπτου (MS) τόσο για τα κράτη "ON" όσο και για "off", τότε ο συνολικός χρόνος για έναν πλήρη κύκλο (μία περίοδο) είναι:
![]()
Η συχνότητα του κύματος μας λέει πόσοι κύκλοι συμβαίνουν ανά δευτερόλεπτο.Για να βρείτε τη συχνότητα, χρησιμοποιήστε τον τύπο:
![]()
Σε αυτή την περίπτωση:
![]()
Έτσι, το κύμα επαναλαμβάνεται 50 φορές ανά δευτερόλεπτο.
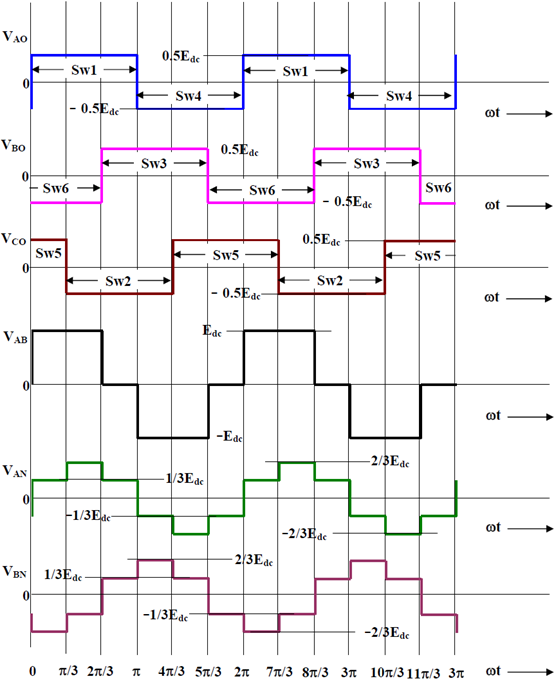
Εικόνα 7: 3-φάση μετατροπέα τάσης με τετραγωνικό κύμα εξόδου
Ορθογώνιο κύμα
Τώρα, ας εξερευνήσουμε ορθογώνιες κυματομορφές, που είναι παρόμοιες με τα τετράγωνα κύματα, αλλά δεν έχουν ίσες και εκτός χρόνου.Ο χρόνος που το σήμα παραμένει υψηλό ονομάζεται το θετικό πλάτος παλμού και ο λόγος εκείνου του χρόνου προς τη συνολική περίοδο ονομάζεται κύκλος λειτουργίας.
Εάν το θετικό πλάτος παλμού είναι 10 ms, αλλά ο κύκλος λειτουργίας είναι 25%, αυτό σημαίνει ότι το κύμα είναι "ON" μόνο για το 25% του συνολικού κύκλου.
Για να βρείτε τη συνολική περίοδο, διαιρέστε το θετικό πλάτος παλμού από τον κύκλο λειτουργίας:
![]()
Για να βρείτε τη συχνότητα, χρησιμοποιήστε τον ίδιο τύπο όπως πριν:
![]()
Έτσι, αυτή η κυματομορφή θα επαναλάβει 25 φορές ανά δευτερόλεπτο με το "on" χρόνο να είναι μικρότερος σε σύγκριση με το χρόνο "εκτός".
Σύγκριση τετραγωνικών κυμάτων, ορθογώνιων κυμάτων και παλμικών κυματομορφών
|
Χαρακτηριστικός |
Τετραγωνικά κύματα |
Ορθογώνια κύματα |
Παλλόμενες κυματομορφές |
|
Σχήμα |
Συμμετρικά, ίσα και χαμηλά χρονικά |
Ασύμμετρη, μεταβαλλόμενος κύκλος λειτουργίας |
Απότομες, απότομες παλμούς διαφορετικού πλάτους |
|
Πλάτος |
Συνεχής |
Συνεχής |
Συνεχής |
|
Συχνότητα |
Διορθώθηκε με βάση την εφαρμογή |
Ευκανόνιστος |
Χαμηλότερη από τη συχνότητα βάσης |
|
Σφυγμός Πλάτος |
Η μισή περίοδος (σε κύκλο εργασίας 50%) |
Εξαρτάται από τον κύκλο λειτουργίας |
Πολύ σύντομο έως μέτριο, ορίζει το παλμό |
|
Επανάληψη Τιμή |
Ορίζεται από τη συχνότητα |
Ορίζεται από τη συχνότητα |
Χαμηλό έως πολύ υψηλό |
|
Δασμός Κύκλος |
50% (σταθερό) |
Οποιοδήποτε ποσοστό, όχι 50% |
Ποικίλλει ευρέως, λιγότερο από 50% |
|
Αρμονικός Περιεχόμενο |
Πλούσιος σε περίεργες αρμονικές |
Πλούσιο σε αρμονικές |
Εξαρτάται από το σχήμα του παλμού και το πλάτος |
|
Παραγωγή Μέθοδος |
Ταλαντωτές, σαγιονάρες |
Ρυθμιζόμενοι ταλαντωτές, γεννήτριες σήματος |
Γεννήτριες παλμών, εξειδικευμένα κυκλώματα |
|
Αιτήσεις |
Κυκλώματα χρονισμού, ψηφιακά ρολόγια |
Εναλλαγή τροφοδοσίας, διαμορφωτές |
Ραντάρ, επικοινωνία, ιατρική απεικόνιση |
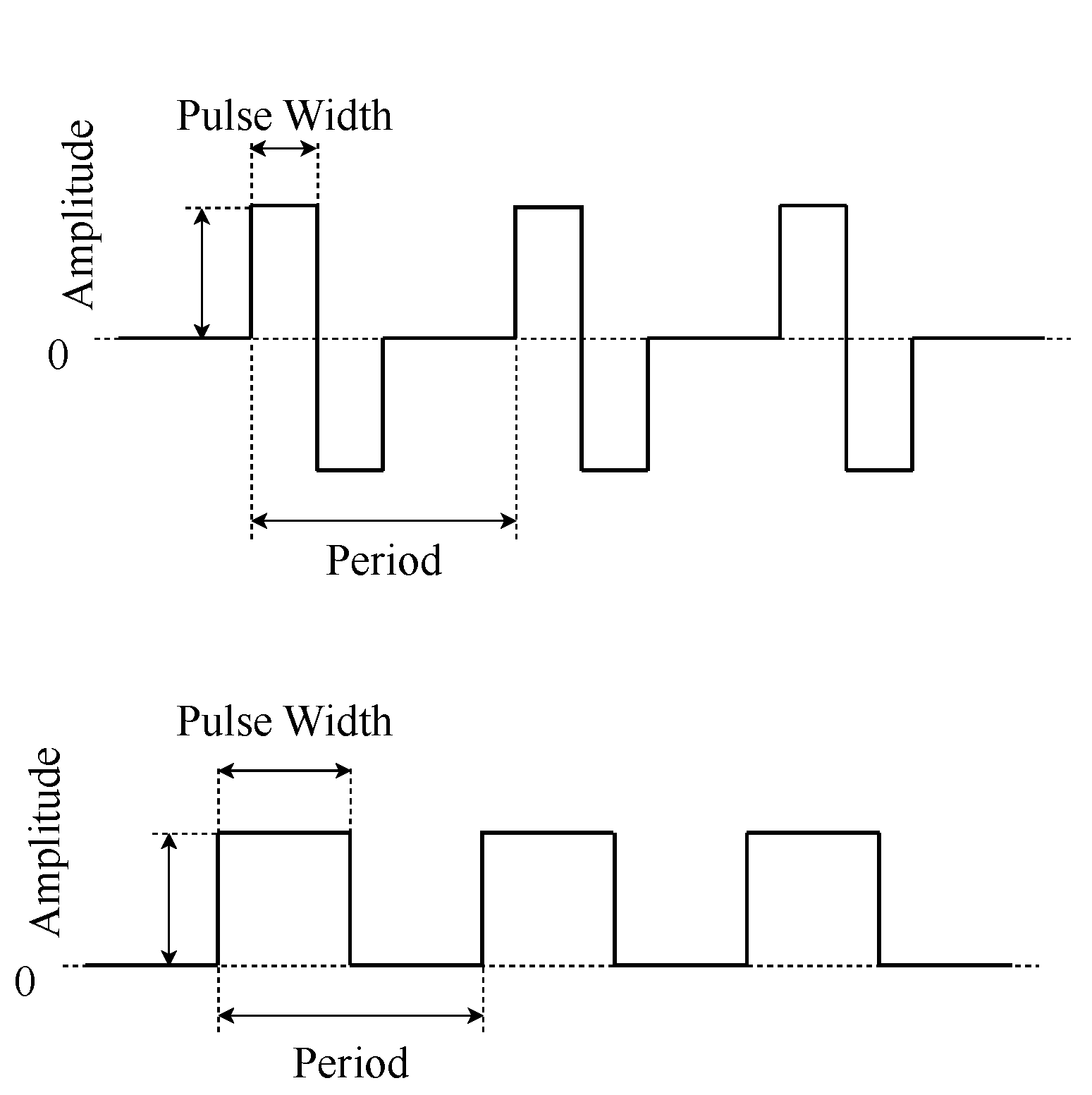
Εικόνα 8: τετράγωνο και ορθογώνιο κύμα
Σύναψη
Αυτό το άρθρο εξηγεί τη σημασία των διαφόρων τύπων κυματομορφών στο σχεδιασμό ηλεκτρονικών συστημάτων.Κάθε κυματομορφή έχει τις δικές της ιδιότητες και οφέλη που είναι χρήσιμα σε συγκεκριμένες καταστάσεις.Τα τετράγωνα κύματα είναι χρήσιμα για τα ψηφιακά συστήματα.Εξασφαλίζουν ομαλές και ακριβείς μεταβάσεις μεταξύ δυαδικών καταστάσεων που είναι καλές για την επεξεργασία δεδομένων και την επικοινωνία.Τα ορθογώνια κύματα επεκτείνονται σε αυτή την έννοια παρέχοντας ρυθμιζόμενους κύκλους λειτουργίας, επιτρέποντας τον ακριβέστερο έλεγχο σε εφαρμογές όπου ο χρονισμός του σήματος πρέπει να προσαρμοστεί.Τα παλμικά κύματα είναι ανεκτίμητα σε καταστάσεις που απαιτούν υψηλή ευελιξία και ανταπόκριση, όπως ραντάρ ή ιατρική απεικόνιση.Μεταφέρουν πληροφορίες μέσω αλλαγών σε σχήμα παλμού και χρονισμό, καθιστώντας τους ιδανικές για τη μετάδοση δεδομένων.Η ανάλυση Fourier αυτών των κυματομορφών προσφέρει μια σαφή, μαθηματική κατανόηση της συμπεριφοράς τους.Αυτό το άρθρο δίνει μια σαφή επισκόπηση τόσο της θεωρίας όσο και των πρακτικών χρήσεων αυτών των κυματομορφών, καθιστώντας τον πολύτιμο οδηγό για όσους εργάζονται σε ηλεκτρονικό σχεδιασμό.
Συχνές ερωτήσεις [FAQ]
1. Ποια είναι τα πλεονεκτήματα των τετραγωνικών κυμάτων;
Τα τετράγωνα κύματα αποτιμώνται επειδή είναι απλά και χρήσιμα σε πολλά ηλεκτρονικά και εργασίες επεξεργασίας σήματος.Ένα μεγάλο όφελος είναι η απότομη αλλαγή τους μεταξύ υψηλών και χαμηλών επιπέδων, καθιστώντας τα τέλεια για χρονισμό και ψηφιακά σήματα ρολογιού σε υπολογιστές και άλλες ψηφιακές συσκευές.Αυτές οι γρήγορες αλλαγές βοηθούν στην αποφυγή σύγχυσης στα σήματα ανάγνωσης.Επίσης, τα τετράγωνα κύματα έχουν μόνο περίεργες αρμονικές που τους καθιστούν ευκολότερο να εργαστούν σε εφαρμογές που περιλαμβάνουν αρμονικές, όπως οι συνθετικοί και η τεχνολογία ήχου, όπου οι σαφείς ήχοι είναι σημαντικοί.
2. Πώς κατασκευάζονται τετράγωνα κύματα;
Τα τετράγωνα κύματα παράγονται χρησιμοποιώντας ηλεκτρονικούς ταλαντωτές, όπως οι ενεργοποιητές Schmitt ή τα κυκλώματα flip-flop, που εναλλάσσονται μεταξύ δύο επιπέδων τάσης.Αυτοί οι ταλαντωτές μεταβάλλουν τις εξόδους όταν η είσοδός τους διασχίζει ορισμένες τιμές κατωφλίου, δημιουργώντας τις αιχμηρές μεταβάσεις που χαρακτηρίζουν τα τετραγωνικά κύματα.Οι γεννήτριες λειτουργιών που χρησιμοποιούνται σε εργαστήρια μπορούν επίσης να προγραμματιστούν για να παράγουν τετράγωνα κύματα της επιθυμητής συχνότητας και πλάτους με ταχέως εναλλαγή μεταξύ καταστάσεων υψηλής και χαμηλής τάσης.
3. Ποια είναι η ορθογώνια περίοδος παλμών;
Η περίοδος ενός ορθογώνιου παλμού αναφέρεται στη διάρκεια ενός πλήρους κύκλου του παλμού, που περιλαμβάνει ένα υψηλό κράτος και μία χαμηλή κατάσταση.Αυτό ποσοτικοποιείται ως ο χρόνος που χρειάζεται για να επιστρέψει ο παλμός στην αρχική του κατάσταση.Η περίοδος t του παλμού είναι το άθροισμα της διάρκειας του υψηλού κράτους (Tthigh) και της χαμηλής κατάστασης (TLOW), που εκφράζεται ως T = μηρός+Tlow.Στην πράξη, αυτή η περίοδος καθορίζει τη συχνότητα της κυματομορφής παλμών με συχνότητα να είναι η αμοιβαία της περιόδου (F = 1/T).
4. Ποια είναι τα συστατικά της κυματομορφής παλμών;
Μια κυματομορφή παλμού αποτελείται από διάφορα εξαρτήματα:
Πλάτος: Η μέγιστη τιμή του παλμού πάνω ή κάτω από τη γραμμή βάσης.
Διάρκεια: Το χρονικό διάστημα για τον παλμό βρίσκεται στο μέγιστο πλάτος του.
Χρόνος αύξησης: Ο χρόνος που απαιτείται για τον παλμό στη μετάβαση από τη χαμηλή τιμή (συχνά αλεσμένη ή μηδενική τάση) στην υψηλή τιμή του.
Χρόνος πτώσης: Ο χρόνος που απαιτείται για τον παλμό να μεταβεί πίσω από την υψηλή του αξία στη χαμηλή τιμή του.
Κύκλος λειτουργίας: αντιπροσωπεύει το ποσοστό μιας περιόδου κατά την οποία το σήμα είναι ενεργό ή υψηλό.Συχνά εκφράζεται ως ποσοστό.
5. Πώς μετράται η κυματομορφή παλμού;
Εδώ είναι η διαδικασία:
Συνδέστε τους ανιχνευτές του παλμογράφου με την πηγή σήματος ή τη συσκευή που εξάγει την κυματομορφή παλμών.
Ρυθμίστε τις ρυθμίσεις του παλμογράφου όπως το Time/Division και το Volts/Division για να μειώσετε κατάλληλα την κυματομορφή στην οθόνη.
Ενεργοποιήστε τον παλμογράφο για τη σταθεροποίηση της οθόνης κυματομορφής, εξασφαλίζοντας ότι ο παλμός είναι καθαρά και σταθερά απεικονίζεται.
Χρησιμοποιήστε τα εργαλεία μέτρησης του παλμογράφου για να προσδιορίσετε το πλάτος, την περίοδο, τον κύκλο λειτουργίας του παλμού, τον χρόνο αύξησης και τον χρόνο πτώσης απευθείας από την εμφανιζόμενη κυματομορφή.
Σχετικά με εμάς
ALLELCO LIMITED
Διαβάστε περισσότερα
Γρήγορη έρευνα
Στείλτε μια ερώτηση, θα απαντήσουμε αμέσως.

Αμαρτωλός
στο 2024/08/27

Τι πρέπει να γνωρίζετε για την ηλεκτρομαγνητική συμβατότητα;
στο 2024/08/27
Δημοφιλείς θέσεις
-
Τι είναι το GND στο κύκλωμα;
στο 1970/01/1 2959
-

Οδηγός σύνδεσης RJ-45: Κωδικοί σύνδεσης RJ-45, Σχέδια καλωδίωσης, Εφαρμογές R-J45, RJ-45 Datasheets
στο 1970/01/1 2513
-

Τύποι σύνδεσης ινών: SC vs LC και LC VS MTP
στο 1970/01/1 2099
-
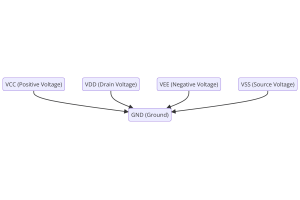
Κατανόηση τάσεων τροφοδοσίας σε ηλεκτρονικά VCC, VDD, VEE, VSS και GND
στο 0400/11/10 1913
-

Σύγκριση μεταξύ DB9 και RS232
στο 1970/01/1 1768
-

Τι είναι η μπαταρία LR44;
Η ηλεκτρική ενέργεια, αυτή η πανταχού παρούσα δύναμη, διαπερνά ήσυχα κάθε πτυχή της καθημερινής μας ζωής, από τα ασήμαντα gadgets έως τον απειλητικό για τη ζωή ιατρική εξοπλισμό, παίζει έναν σιωπηλό ρόλο.Ωστόσο, η πραγματικ...στο 1970/01/1 1717
-

Κατανόηση των θεμελιωδών στοιχείων: Αντίσταση επαγωγής, και καταφύγιο
Στον περίπλοκο χορό της Ηλεκτρολόγων Μηχανικών, ένα τρίο θεμελιωδών στοιχείων παίρνει το κεντρικό στάδιο: επαγωγή, αντίσταση και χωρητικότητα.Κάθε φέρει μοναδικά χαρακτηριστικά που υπαγορεύουν τους δυναμικούς ρυθμο...στο 1970/01/1 1667
-

CR2430 Περιεκτικός οδηγός μπαταρίας: Προδιαγραφές, εφαρμογές και σύγκριση με μπαταρίες CR2032
Τι είναι η μπαταρία CR2430;Οφέλη από μπαταρίες CR2430ΚανόναςΕφαρμογές μπαταρίας CR2430CR2430 ισοδύναμοCR2430 VS CR2032Μέγεθος μπαταρίας CR2430Τι να ψάξετε όταν αγοράζετε το CR2430 και τα ισοδύναμαΦύλλο δεδομένων PDFΣυχνές ερωτήσεις Οι μπαταρ...στο 1970/01/1 1583
-
Τι είναι το RF και γιατί το χρησιμοποιούμε;
Η τεχνολογία ραδιοσυχνότητας (RF) αποτελεί βασικό μέρος της σύγχρονης ασύρματης επικοινωνίας, επιτρέποντας τη μετάδοση δεδομένων σε μεγάλες αποστάσεις χωρίς φυσικές συνδέσεις.Αυτό το άρθρο βυθίζεται στα βασικά του RF, ...στο 1970/01/1 1555
-

CR2450 VS CR2032: Μπορεί να χρησιμοποιηθεί η μπαταρία;
Οι μπαταρίες του μαγγανίου λιθίου έχουν κάποιες ομοιότητες με άλλες μπαταρίες λιθίου.Η υψηλή ενεργειακή πυκνότητα και η μακρά διάρκεια ζωής είναι τα χαρακτηριστικά που έχουν κοινό.Αυτό το είδος μπαταρίας έχει κερδίσε...στο 1970/01/1 1522
















































