Σπίτι Blog~~Λεπτομερής οδηγός για τον πλήρη αθροιστή~~

~~στο 2024/05/10~~ ~~602~~

Λεπτομερής οδηγός για τον πλήρη αθροιστή

Στη σφαίρα της ψηφιακής ηλεκτρονικής και της μηχανικής ηλεκτρονικών υπολογιστών, τα adders αντιπροσωπεύουν ένα από τα πιο βασικά δομικά στοιχεία, ζωτικής σημασίας στην κατασκευή και τη λειτουργικότητα των πιο περίπλοκων αριθμητικών κυκλωμάτων.Ως ολοκληρωμένα στοιχεία της αριθμητικής λογικής μονάδας (ALU), οι πρόσθετες διευκολύνουν πολυάριθμες υπολογιστικές λειτουργίες, που κυμαίνονται από βασικές αριθμητικές έως σύνθετες λογικές εργασίες που απαιτούνται για τις λειτουργίες του συστήματος.Ο σχεδιασμός τους, ο οποίος μπορεί να διαφέρει από τους απλούς μισούς προσθέτες σε πιο πολύπλοκα πλήρη adpers, διαδραματίζει καθοριστικό ρόλο στην ενίσχυση της αποτελεσματικότητας και της ταχύτητας επεξεργασίας εντός των ψηφιακών συστημάτων.Αυτό το άρθρο βυθίζεται στη λεπτομερή αρχιτεκτονική και τις λειτουργικές αποχρώσεις των διαφόρων τύπων προστάτη, απεικονίζοντας τον κρίσιμο ρόλο τους στη σύγχρονη τεχνολογία υπολογιστών και εξερευνώντας τη λειτουργική τους λογική, κυκλώματα και εφαρμογές στο ευρύτερο πλαίσιο της ψηφιακής λογικής σχεδιασμού.

Κατάλογος

1. Τι είναι ο προστάτης;

2. μισός αθροιστής

3. Πλήρης αθροιστής

4. Πίνακας πλήρους αθροιστή αλήθειας

5. Χαρακτηριστικά εξισώσεις ενός πλήρους αθροιστή

6. Εφαρμογή ενός πλήρους κυκλώματος αθροίσματος

7. Πλεονεκτήματα και μειονεκτήματα των πλήρους προσανατολισμού

8. Εφαρμογές πλήρους adpers στην ψηφιακή λογική

9. Παραδείγματα εφαρμογών πλήρους αθροίσματος

10. Συμπέρασμα

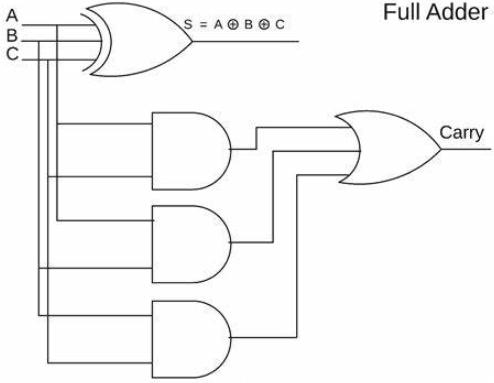
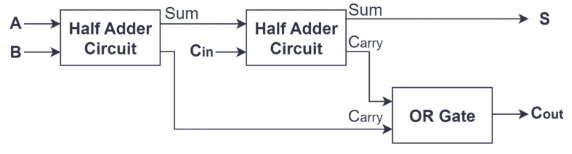
Εικόνα 1: Πλήρης αθροιστής

Τι είναι ο αθροιστής;

Ένας αθροιστής είναι ένα θεμελιώδες στοιχείο στον τομέα της ηλεκτρονικής μηχανικής και της ψηφιακής λογικής και παίζει κεντρικό ρόλο σε πιο σύνθετα συστήματα υπολογιστών.Ως μέρος της αριθμητικής λογικής μονάδας (ALU), ο προστάτης χειρίζεται μια ποικιλία βασικών εργασιών υπολογιστών.Η αποτελεσματικότητα και η απόδοση ολόκληρου του επεξεργαστή επηρεάζονται άμεσα από το σχεδιασμό και τη λειτουργικότητα του αθροιστή.

Στον επεξεργαστή, ο αθροιστής χρησιμοποιείται όχι μόνο για βασικές αριθμητικές λειτουργίες όπως η προσθήκη και η αφαίρεση, αλλά και ασχολείται με ένα ευρύτερο φάσμα λογικών λειτουργιών.Για παράδειγμα, κατά την εκτέλεση προγραμμάτων, ο επεξεργαστής πρέπει συχνά να υπολογίσει νέες διευθύνσεις μνήμης.Αυτό γίνεται συνήθως με την προσθήκη ή την αφαίρεση από την τρέχουσα διεύθυνση - μια εργασία που αναλαμβάνεται από τον αθροιστή.Ελέγχουν τον αριθμό των επαναλήψεων βρόχου και τη συνολική ροή αυξάνοντας και μειώνοντας τους μετρητές.Σε πιο πολύπλοκες εφαρμογές, όπως η ευρετηρίαση πίνακα, οι πρόσθετες εντοπίζουν γρήγορα δεδομένα υπολογίζοντας αντισταθμίσεις.Αυτό είναι σημαντικό για τα συστήματα διαχείρισης βάσεων δεδομένων, την κατασκευή μεταγλωττιστή και την επεξεργασία δεδομένων μεγάλης κλίμακας.Οι πρόσθετοι είναι επίσης καθοριστικοί για την εφαρμογή ορισμένων τεχνικών χαρτογράφησης σε συστήματα προσωρινής μνήμης πολλαπλών επιπέδων, χρησιμοποιώντας αριθμητικές λειτουργίες για τον προσδιορισμό της θέσης των δεδομένων στην προσωρινή μνήμη, βελτιστοποιώντας έτσι την αποτελεσματικότητα της πρόσβασης.

Τεχνολογικά, οι πρόσθετες υλοποιούνται μέσω διαφόρων σχεδίων κυκλώματος, συμπεριλαμβανομένων των παραλληλισμών, σειριακών και αγωγών.Τα παράλληλα adpers ευνοούνται για την ικανότητά τους να χειρίζονται ταυτόχρονα πολλαπλά ψηφία, καθιστώντας τα κατάλληλα για σενάρια που απαιτούν γρήγορο υπολογισμό.Από την άλλη πλευρά, επεξεργάζονται ένα bit ανά κύκλο ρολογιού και είναι ιδανικοί για περιβάλλοντα περιορισμένου ή χαμηλής ισχύος.Οι πρόσθετοι αγωγών διαιρούν τη διαδικασία προσθήκης σε διάφορα στάδια, κάθε χειρισμό ενός μέρους της λειτουργίας προσθήκης.Αυτός ο σχεδιασμός ενισχύει σημαντικά την ταχύτητα υπολογισμού, ειδικά σε περιβάλλοντα υπολογιστών υψηλής απόδοσης.

Ημιαθροϊστής

Ένα κύκλωμα μισού προστάτη είναι ένα θεμελιώδες δομικό στοιχείο σε ψηφιακά ηλεκτρονικά, ειδικά σχεδιασμένα για να προσθέσουν δύο μονά δυαδικά ψηφία.Αυτό το κύκλωμα σχηματίζει το θεμέλιο ενός πλήρους αθροιστή και είναι το κλειδί για την κατανόηση πιο σύνθετων σχεδίων κυκλώματος λογικής.Σε ένα μισό αθροιστή, υπάρχουν δύο πρωταρχικές εισόδους, με την ένδειξη Α και Β, οι οποίες αντιπροσωπεύουν το augend και το προσθήκη αντίστοιχα.Αυτή η ρύθμιση του επιτρέπει να υπολογίζει το άθροισμα και να μεταφέρει την έξοδο χωρίς την ανάγκη εισόδου μεταφοράς από προηγούμενους υπολογισμούς.

Ο πυρήνας ενός μισού ανάρτηση αποτελείται από δύο λογικές πύλες: μια πύλη XOR και μια πύλη.Η πύλη XOR είναι υπεύθυνη για τη δημιουργία της εξόδου αθροίσματος.Λειτουργεί με έναν απλό κανόνα όπου εξάγει ένα 1 εάν μόνο μία από τις εισροές του είναι 1.Διαφορετικά, εξάγει ένα 0. Η πύλη, από την άλλη πλευρά, χειρίζεται την έξοδο μεταφοράς.Παράγει 1 μόνο όταν και οι δύο εισροές είναι 1, ευθυγραμμίζοντας τέλεια με τις θεμελιώδεις απαιτήσεις της δυαδικής προσθήκης.

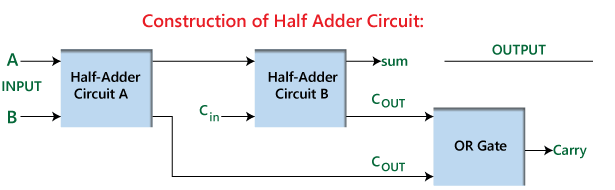
Εικόνα 2: Κατασκευή μισού αθροιστή

Αυτός ο αποτελεσματικός και απλός σχεδιασμός επιτρέπει στον μισό αθροιστή όχι μόνο να εκτελεί ανεξάρτητα δυαδική προσθήκη, αλλά και να χρησιμεύσει ως δομικό στοιχείο για τη δημιουργία ενός πλήρους αθροιστή.Ένας πλήρης αθροιστής κατασκευάζεται συνδυάζοντας δύο μισούς προστάτες με μια επιπλέον ή πύλη.Σε αυτή τη ρύθμιση, το πρώτο εξάμηνο αθροιστής αναλαμβάνει την αρχική εργασία προσθήκης, δημιουργώντας ένα προκαταρκτικό ποσό και μεταφορά.Το δεύτερο ημίχρονο αθροιστής στη συνέχεια επεξεργάζεται τη μεταφορά από την πρώτη μαζί με μια πρόσθετη είσοδο μεταφοράς.Τέλος, η πύλη ή η πύλη συγχωνεύει τις δύο εξόδους μεταφοράς για να παράγουν την τελική έξοδο μεταφοράς.Αυτή η διάταξη ενισχύει τη λειτουργικότητα του αθροιστή, επιτρέποντάς του να χειριστεί πιο σύνθετες εργασίες προσθήκης πολλαπλών ψηφίων, παρουσιάζοντας την ευρεία εφαρμογή και τη σημασία των μισών προσθετικών στο σχεδιασμό ψηφιακού κυκλώματος.

Πλήρης αθροιστής

Ένας πλήρης αθροιστής είναι ένα προηγμένο στοιχείο στο σχεδιασμό ψηφιακής λογικής, εξοπλισμένο για να χειριστεί την προσθήκη τριών δυαδικών εισόδων ενός bit, που συνήθως επισημαίνονται ως Α, Β και μεταφορά (CIN).Αυτός ο σχεδιασμός επιτρέπει στον πλήρη αθροιστή να επεξεργάζεται αποτελεσματικά σύνθετες δυαδικές προσθήκες ενσωματώνοντας τη μεταφορά από προηγούμενους υπολογισμούς χαμηλότερης τάξης σε μία μόνο λειτουργία.

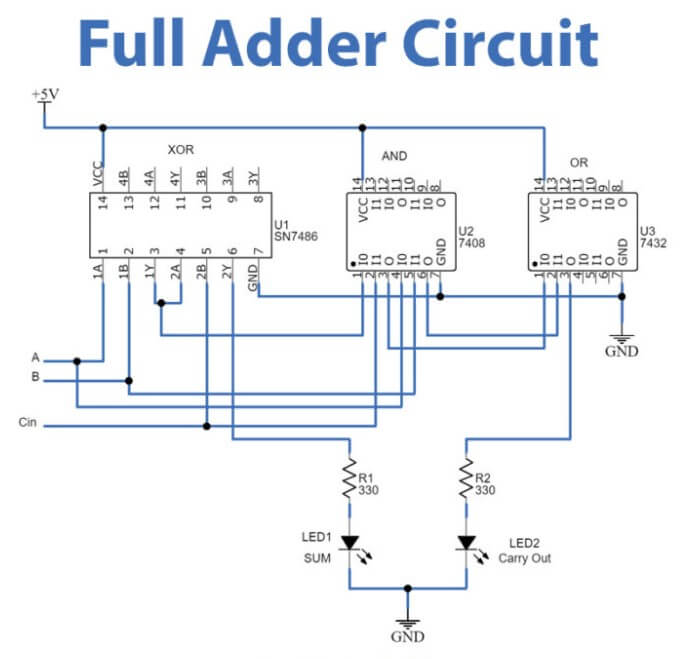
Εικόνα 3: Πλήρες κύκλωμα αθροίσματος

Λειτουργικά, ένας πλήρης αθροιστής μπορεί να εξάγει ένα διψήφιο ποσό, το οποίο σημαίνει ότι η παραγωγή του μπορεί να κυμαίνεται από 0 έως 3 και μπορεί επίσης να παράγει μια μεταφορά (cout).Αυτό συμβαίνει επειδή, όταν όλα τα bits εισόδου έχουν οριστεί σε 1 (a = 1, b = 1, cin = 1), η έξοδος αθροίσματος θα είναι 1 (που αντιπροσωπεύει το δυαδικό 01) και δημιουργείται μεταφορά 1, υποδεικνύοντας ότιΜια πρόσθετη μεταφορά πρέπει να περάσει στο επόμενο υψηλότερο κομμάτι.

Δομικά, ο πλήρης αθροιστής αποτελείται γενικά από δύο μισά advers και ένα ή πύλη.Ο αθροιστής του πρώτου ημιχρόνου λαμβάνει εισόδους Α και Β, δημιουργώντας ένα αρχικό ποσό και ένα σήμα μεταφοράς.Αυτό το αρχικό ποσό τροφοδοτείται στη συνέχεια, μαζί με το carry-in (CIN), στο δεύτερο ημίχρονο.Ο ρόλος του δεύτερου ημιχρόνου είναι να προσθέσει αυτό το ποσό από το πρώτο εξάμηνο αθροιστή στο CIN, παράγοντας ένα άλλο ποσό και μια νέα έξοδο μεταφοράς.Ταυτόχρονα, η έξοδος μεταφοράς από το πρώτο εξάμηνο αθροιστής και η έξοδος μεταφοράς από το δεύτερο ημίχρονο συνδέονται μέσω μιας πύλης, με αποκορύφωμα την τελική μεταφορά (cout) του πλήρους αθροιστή.Ο σχεδιασμός αυτής της δομής εξασφαλίζει ότι ο πλήρης αθροιστής χειρίζεται αποτελεσματικά τη διάδοση των μεταφορέων επιπλέον των εργασιών, καθιστώντας το ιδανικό για την εκτέλεση δυαδικών προσθηκών πολλαπλών ψηφίων.Έτσι, ο σχεδιασμός του πλήρους αθροιστή όχι μόνο επιταχύνει την επεξεργασία δεδομένων και ενισχύει την αποτελεσματικότητα αλλά και απλοποιεί την πολυπλοκότητα της υλοποίησης του υλικού μέσω ενός απλού συνδυασμού λογικών πύλων, καθιστώντας το ένα απαραίτητο στοιχείο στην πολυψήφια προσθήκη και την αριθμητική λογική μονάδα (Alu).

Παραμέτρους	Ημιαθροϊστής	Πλήρης αθροιστής
Περιγραφή	Ο μισός αθροιστής είναι μια συνδυαστική λογική Κύκλωμα που προσθέτει δύο ψηφία 1-bit.Το μισό προστάτη παράγει ένα ποσό των δύο εισόδους.	Ένας πλήρης αθροιστής είναι μια συνδυαστική λογική Το κύκλωμα που εκτελεί μια λειτουργία προσθήκης σε τρεις δυαδικούς αριθμούς ενός bit. Ο πλήρης αθροιστής παράγει ένα άθροισμα των τριών εισροών και της τιμής μεταφοράς.
Προηγούμενος	Η προηγούμενη μεταφορά δεν χρησιμοποιείται.	Χρησιμοποιείται η προηγούμενη μεταφορά.
Εισροές	Στο μισό αθροιστή, υπάρχουν δύο bits εισόδου (a, ΣΙ).	Σε πλήρη αθροιστή, υπάρχουν τρία κομμάτια εισόδου (A, B, C_σε).
Εξόδους	Η παραγόμενη έξοδος είναι δύο bits-sum και μεταφέρετε από την είσοδο 2 bits.	Η παραγόμενη έξοδος είναι δύο bits-sum και μεταφέρετε από την είσοδο 3 bits.
Χρησιμοποιείται ως	Ένα κύκλωμα μισού προστάτη δεν μπορεί να χρησιμοποιηθεί στο με τον ίδιο τρόπο όπως ένα κύκλωμα πλήρους προστάτη.	Ένα πλήρες κύκλωμα ατόμων μπορεί να χρησιμοποιηθεί στη θέση του ενός μισού κυκλώματος αθροίσματος.
Χαρακτηριστικό	Είναι απλό και εύκολο στην υλοποίηση	Ο σχεδιασμός ενός πλήρους αθροιστή δεν είναι Απλό ως μισό αθροιστή.
Λογική έκφραση	Η λογική έκφραση για το μισό αθροιστή είναι: S = a⊕b;C = a*b.	Η λογική έκφραση για πλήρη αθροιστή είναι: S = a⊕b⊕cin;ντο_έξω= (ab)+(c_σε(a⊕b)).
Λογικές πύλες	Αποτελείται από μία πρώην πύλη και μία και πύλη.	Αποτελείται από δύο πρώην ή δύο πύλες, και μία ή πύλη.
Αιτήσεις	Χρησιμοποιείται σε αριθμομηχανές, υπολογιστές, ψηφιακές συσκευές μέτρησης, κ.λπ.	Χρησιμοποιείται σε προσθήκες πολλαπλών δυαδικών ψηφίων, ψηφιακοί επεξεργαστές, κ.λπ.
Εναλλακτικό όνομα	Δεν υπάρχει εναλλακτικό όνομα για το ήμισυ αθροιστής.	Ένας πλήρης αθροιστής είναι επίσης γνωστός ως κυματομορφή αθροιστής.

Διάγραμμα 1: Διαφορά μεταξύ του μισού αθροιστή και του πλήρους αθροιστή

Πλήρης τραπέζι της αλήθειας

Ο πίνακας αλήθειας ενός πλήρους αθροιστή είναι το κλειδί για την κατανόηση της λειτουργικής του λογικής, περιγράφοντας λεπτομερώς την ακριβή σχέση μεταξύ των συνδυασμών δυαδικών εισροών και των αντίστοιχων εξόδων τους.Αυτός ο πίνακας καταδεικνύει όλα τα πιθανά σενάρια εισροών και τα αποτελέσματά τους, καθιστώντας το βασικό εργαλείο για το σχεδιασμό και την επαλήθευση των κυκλωμάτων ψηφιακής λογικής.Ο πλήρης αθροιστής επεξεργάζεται τρεις εισόδους: A, B και A Carry-in (CIN), καθένα από τα οποία μπορεί να είναι είτε 0 είτε 1. Αυτό έχει ως αποτέλεσμα οκτώ πιθανούς συνδυασμούς εισροών.

Για κάθε έναν από αυτούς τους συνδυασμούς, οι εξόδους από τον πλήρη αθροιστή περιλαμβάνουν ένα άθροισμα (άθροισμα) και μια μεταφορά (cout).Το άθροισμα είναι η προσθήκη Modulo-2 (λειτουργία XOR) των τριών εισόδων-Α, Β και CIN.Η μεταφορά εμφανίζεται όταν τουλάχιστον δύο από τα bits εισόδου είναι 1. Αυτό αντικατοπτρίζει την ικανότητα του πλήρους αθροιστή να χειριστεί τη μεταφορά σε λειτουργίες διαδοχικής προσθήκης, εξασφαλίζοντας την ακρίβεια σε υπολογισμούς υψηλότερου bit.

Για να το δείξετε, εξετάστε το σενάριο εισόδου όπου όλες οι εισόδους είναι 0 (a = 0, b = 0, c-in = 0).Το άθροισμα εξόδου θα είναι 0, και η μεταφορά θα είναι επίσης 0, υποδεικνύοντας ότι δεν υπάρχει πρόσθετο ποσό ή μεταφορά για να διαχειριστεί.Εάν μόνο ένα bit εισόδου είναι 1, όπως a = 1, b = 0, c-in = 0, το άθροισμα εξόδου θα είναι 1 χωρίς καμία μεταφορά, δείχνοντας ότι δεν χρειάζεται να μεταφέρετε μια μεταφορά σε υψηλότερο κομμάτι.Όταν δύο bits εισόδου είναι 1, όπως a = 1, b = 1, c-in = 0, το άθροισμα εξόδου είναι 0 (δεδομένου ότι το 1+1 ισούται με 2 σε δυαδικό και το modulo-2 έχει ως αποτέλεσμα 0), αλλά η μεταφοράΤο Out είναι 1, υποδεικνύοντας μια μεταφορά που πρέπει να περάσει στο επόμενο υψηλότερο κομμάτι.Το πιο περίπλοκο σενάριο εμφανίζεται όταν και τα τρία bits εισόδου είναι 1 (a = 1, b = 1, c-in = 1).Το άθροισμα εξόδου είναι 1, και υπάρχει μια μεταφορά του 1, υποδηλώνοντας ότι η διαχείριση μεταφοράς μπορεί επίσης να απαιτείται σε ακόμη υψηλότερα bits.

ΕΝΑ	σι	ντο_σε	μικρό	ντο_έξω
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Διάγραμμα 2: Πίνακας πλήρους αθροιστή αλήθειας

Χαρακτηριστικά εξισώσεις ενός πλήρους αθροιστή

Η κατανόηση του πλήρους αθροιστή συνεπάγεται τη διαίρεση της λειτουργικότητάς του χρησιμοποιώντας τον πίνακα αλήθειας, όπου διαφορετικοί συνδυασμοί τιμών εισροών Α, Β και C-in οδηγούν σε έξοδο και cout.Για να κατανοήσουμε τη λειτουργία, απλοποιούμε τις λογικές εξισώσεις βήμα προς βήμα.

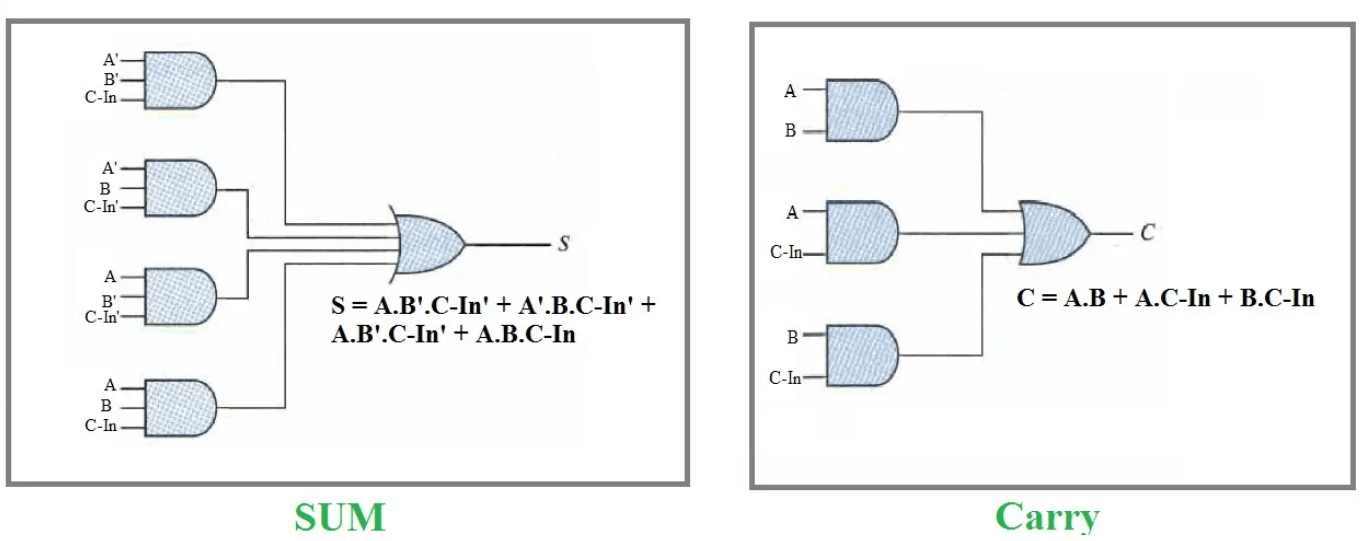
Λογική έκφραση για άθροισμα

Η εξίσωση ξεκινά με τις ξεχωριστές περιπτώσεις όπου το άθροισμα ισούται με 1:

• a 'b' cin + a 'b cin' + a b 'cin' + ab cin

Αυτή η εξίσωση μπορεί να συμπυκνωθεί με ομαδοποίηση όρων με και χωρίς CIN:

• CIN (A 'B' + AB) + CIN '(A' B + A B ')

Αυτή η απλούστευση οδηγεί σε μια μορφή ευκολότερης εφαρμογής:

• CIN XOR (A XOR B)

Αυτή η αναπαράσταση δείχνει ότι η έξοδος του αθροίσματος είναι ουσιαστικά η λειτουργία XOR μεταξύ Α, Β και CIN, καταγράφοντας τη βασική συμπεριφορά της δυαδικής προσθήκης όπου το άθροισμα αναδύεται με βάση έναν περίεργο αριθμό.

Λογική για cout

Ξεκινώντας με συνθήκες όπου δημιουργείται η μεταφορά:

• A 'B CIN + A B' CIN + AB C-in ' + AB CIN

Απλοποίηση της εξίσωσης, προσδιορίζουμε όρους που συνήθως περιλαμβάνουν τη δημιουργία μιας μεταφοράς:

• ab + b cin + a cin

Ψάχνετε για μια άλλη μέθοδο για την εφαρμογή του COUT, η εξίσωση μπορεί να αναδιαμορφωθεί:

• ab + a cin + b c-in (a + a ')

Αυτό επεκτείνεται και ανασυνδυάζει για να συλλάβει όλα τα σενάρια όπου τουλάχιστον δύο εισροές είναι 1:

• ab cin + ab + a c-in + a 'b cin

• AB (1 + CIN) + A C-In + A 'B CIN

• ab + a c-in (b + b ') + a' b cin

• ab + a b 'cin + a' b cin

• AB + CIN (A 'B + A B')

Η τελική συμπαγής μορφή για το cout:

• AB + CIN (A XOR B)

Αυτή η έκδοση της εξίσωσης μεταφοράς καταδεικνύει πώς παράγεται το COUT είτε όταν και οι δύο a και b είναι 1, ή όταν ένα από το a ή b είναι 1 μαζί με μια μεταφορά, ενθυλάκοντας έτσι τη λογική που απαιτείται για τη διαχείριση της διάδοσης μεταφοράς σε multi-δυαδική προσθήκη.Αυτή η απλοποιημένη λογική είναι ιδιαίτερα χρήσιμη για την εφαρμογή αποτελεσματικών ψηφιακών κυκλωμάτων.

Εικόνα 4: Εξισώσεις ενός πλήρους αθροιστή

Εφαρμογή πλήρους κυκλώματος αθροίσματος

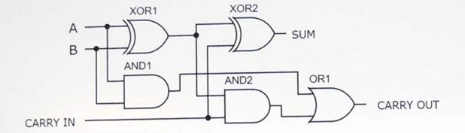
Η εφαρμογή ενός πλήρους κυκλώματος αθροιστή περιλαμβάνει προσεκτικά τη συναρμολόγηση δύο μισών advers και μιας πύλης για να δημιουργήσει μια συσκευή ικανή να χειριστεί αποτελεσματικά την προσθήκη τριών δυαδικών εισόδων ενός bit.Αυτή η διάταξη βελτιστοποιεί την πολυπλοκότητα του κυκλώματος και εξασφαλίζει τόσο αποτελεσματικούς όσο και ακριβείς υπολογισμούς.

Για να ξεκινήσετε, το πρώτο εξάμηνο αθροιστής παίρνει δύο πρωταρχικές δυαδικές εισόδους, Α και Β, τα οποία είναι τα κύρια ψηφία που πρέπει να προστεθούν.Το βασικό του καθήκον είναι να υπολογίσει το άθροισμα και την αρχική μεταφορά αυτών των δύο αριθμών.Εδώ, το πρώτο εξάμηνο αθροιστής παραδίδει δύο αποτελέσματα: ένα αρχικό άθροισμα (sum1) και ένα αρχικό μεταφορά (carry1).Το SUM1 προέρχεται από τη λειτουργία XOR των Α και Β, υποδεικνύοντας αν το σύνολο έχει ένα περίεργο αριθμό 1.Το Carry1, το αποτέλεσμα της λειτουργίας και της λειτουργίας μεταξύ Α και Β, υποδεικνύει αν και τα δύο ψηφία είναι 1, που απαιτούν τη μεταφορά στο επόμενο υψηλότερο κομμάτι.

Στη συνέχεια, ο δεύτερος μισός αθροιστής ενώνει τη διαδικασία.Χρησιμοποιεί το άθροισμα αθροίσματος Sum1 και το τρίτο εισόδου CIN (μεταφορά από προηγούμενο υπολογισμό) ως εισροές του.Το δεύτερο ημίχρονο προσελκύει δύο εξόδους: το τελικό αποτέλεσμα Sum (SUM2) και το δευτερεύον μεταφορά (Carry2).Το SUM2, το οποίο είναι το αποτέλεσμα XOR των SUM1 και CIN, αντιπροσωπεύει το τελικό άθροισμα των τριών εισροών, εμφανίζοντας τη συγκεντρωτική δυαδική προσθήκη.Το Carry2, που αναδύεται από το και τη λειτουργία μεταξύ Sum1 και Cin, υποδεικνύει μια μεταφορά που παράγεται από αυτά τα εξαρτήματα.

Full Adder Circuit with Using Two Half Adder

Εικόνα 5: Πλήρες κύκλωμα ατόμων με τη χρήση δύο μισών αθροίσματος

Τέλος, για να ολοκληρωθεί ο σχεδιασμός του πλήρους αθροιστή, μια πύλη ή πύλη απαιτείται για να χειριστεί τις εξόδους μεταφοράς Carry1 και Carry2 και από τα δύο μισά adpers.Αυτή η πύλη ή η πύλη εξασφαλίζει ότι οποιαδήποτε μεταφορά που παράγεται κατά τη διάρκεια των υπολογισμών προωθείται σωστά στην τελική έξοδο.Επομένως, η τελική έξοδος μεταφοράς του πλήρους αθροιστή (COUT) είναι το αποτέλεσμα Carry1 και Carry2.Η συμπερίληψη αυτού ή της πύλης εγγυάται ότι όλες οι δυνητικές μεταφορές υπολογίζονται με ακρίβεια και μεταφέρονται στο επόμενο επίπεδο σε λειτουργίες προσθήκης πολλαπλών ψηφίων, εξασφαλίζοντας την ακεραιότητα της αριθμητικής λειτουργίας σε πολλαπλά bits.

Πλεονεκτήματα και προκλήσεις πλήρους adders στην ψηφιακή λογική

Οι πλήρεις adders διαδραματίζουν έναν απαραίτητο ρόλο στον σχεδιασμό της ψηφιακής λογικής, προσφέροντας πολλά οφέλη που τα καθιστούν απαραίτητα σε διάφορα σενάρια υπολογιστικής και επεξεργασίας δεδομένων.Τα κύρια πλεονεκτήματά τους περιλαμβάνουν αξιοσημείωτη ευελιξία, ταχύτητες επεξεργασίας γρήγορης επεξεργασίας και αποτελεσματική διαχείριση μεταφοράς.Αυτά τα χαρακτηριστικά καθιστούν πλήρη πρόσθετα ιδανικά για την εκτέλεση σύνθετων αριθμητικών λειτουργιών και λογικών λειτουργιών, ιδιαίτερα σε εφαρμογές που απαιτούν διαδοχική προσθήκη πολλαπλών ψηφίων.

Φόντα

Ευελιξία: Οι πλήρεις adders υπερέχουν στην ικανότητά τους να επεξεργάζονται ταυτόχρονα πολλαπλές δυαδικές εισόδους (A, B και CIN).Μπορούν επίσης να επεκταθούν σε μεγαλύτερες συστοιχίες αθροίσματος για να χειριστούν μεγαλύτερους δυαδικούς αριθμούς.Αυτή η επεκτασιμότητα είναι σημαντική για την οικοδόμηση αριθμητικών λογικών μονάδων υψηλής απόδοσης (ALUS), οι οποίες πρέπει να εκτελούν περίπλοκες αριθμητικές και λογικές λειτουργίες πολλαπλών ψηφίων.

Ταχύτητα: Χάρη στην εσωτερική τους αρχιτεκτονική επεξεργασίας, οι πλήρεις adpers μπορούν να ολοκληρώσουν την προσθήκη όλων των εισροών σε έναν κύκλο ρολογιού, ενώ παράλληλα καθορίζουν τις εξόδους μεταφοράς.Αυτή η δυνατότητα υποστηρίζει λειτουργίες συνεχούς προσθήκης και είναι απαραίτητη για την επεξεργασία δεδομένων σε πραγματικό χρόνο σε σύγχρονους μικροεπεξεργαστές και υπολογιστικές συσκευές υψηλής ταχύτητας.

Μειονεκτήματα

Ωστόσο, οι πλήρεις adders παρουσιάζουν επίσης αξιοσημείωτα μειονεκτήματα:

Πολυπλοκότητα στο σχεδιασμό και την υλοποίηση: Οι πλήρεις adpers περιλαμβάνουν πολλαπλές λογικές πύλες και πολλαπλές διατάξεις μεταφοράς, καθιστώντας το σχεδιαστικό τους συγκρότημα.Αυτή η πολυπλοκότητα όχι μόνο αυξάνει το κόστος κατασκευής αλλά μπορεί επίσης να επηρεάσει την αξιοπιστία των κυκλωμάτων.

Θέματα καθυστέρησης διάδοσης: Η διάδοση της μεταφοράς μπορεί να περάσει από αρκετές λογικές πύλες, προσθέτοντας την καθυστέρηση του.Αυτό μπορεί να περιορίσει τη συνολική υπολογιστική ταχύτητα κατά τη διάρκεια μεγάλης κλίμακας λειτουργίες, ιδιαίτερα σε εκτεταμένα συστήματα πληροφορικής και στο σχεδιασμό της πολύ μεγάλης κλίμακας ενσωμάτωσης (VLSI) και των επεξεργαστών υψηλής ταχύτητας.Η καθυστέρηση μπορεί να γίνει μια σημαντική συμφόρηση στην απόδοση.

Για να μετριάσουν αυτά τα ζητήματα, οι μηχανικοί διερευνούν συνεχώς πιο αποτελεσματικά σχέδια κυκλώματος.Οι στρατηγικές περιλαμβάνουν τη χρήση ταχύτερων τεχνολογιών λογικής πύλης, βελτιστοποίησης των διατάξεων κυκλωμάτων για τη συντόμευση των μήκους διαδρομής και την ανάπτυξη προηγμένων τεχνολογιών όπως οι προστασίες μεταφοράς για να ελαχιστοποιηθούν οι καθυστερήσεις στη διάδοση μεταφοράς.

Εφαρμογές πλήρους adders στην ψηφιακή λογική

Οι πλήρεις adpers χρησιμοποιούνται εκτενώς στην ψηφιακή λογική, βραβευμένες για την ευελιξία και την αποτελεσματικότητά τους, καθιστώντας τους κεντρικούς σε ένα πλήθος εργασιών υπολογιστικής και επεξεργασίας δεδομένων.Η εφαρμογή τους καλύπτει από βασικές αριθμητικές λειτουργίες έως πολύπλοκη επεξεργασία σήματος και έλεγχο του συστήματος.Ακολουθεί μια λεπτομερής ματιά σε ορισμένους βασικούς τομείς όπου οι πλήρεις πρόσθετες είναι αναπόσπαστες.

Αριθμητικά κυκλώματα

Μία από τις πιο απλές χρήσεις των πλήρων προσθετικών είναι τα αριθμητικά κυκλώματα όπου εκτελούν δυαδική προσθήκη.Ιδιαίτερα ζωτικής σημασίας σε προσθήκη αριθμών πολλαπλών ψηφίων, οι πλήρεις adders διαχειρίζονται μακρύτερες δυαδικές ακολουθίες μέσω του cascading.Σε αυτή τη ρύθμιση, κάθε πλήρης αθροιστής χειρίζεται την προσθήκη για τη θέση του bit και τη μεταφορά από το κάτω bit και στη συνέχεια περνάει τη νέα μεταφορά στον πλήρη αθροιστή του επόμενου υψηλότερου bit.Αυτός ο καταρράκτης επιτρέπει την ολοκληρωμένη προσθήκη πολλαπλών ψηφίων σε ολόκληρο το φάσμα των ψηφίων.

Επεξεργασία δεδομένων

Οι πλήρεις πρόσθετοι διαδραματίζουν επίσης κεντρικό ρόλο στις προηγμένες εργασίες επεξεργασίας δεδομένων, όπως η επεξεργασία ψηφιακού σήματος (DSP) για μετασχηματισμό φιλτραρίσματος και μετασχηματισμού Fourier, όπου απαιτούνται ακριβείς και γρήγορες αριθμητικές λειτουργίες.Επιπλέον, στον τομέα της ασφάλειας των πληροφοριών, συμπεριλαμβανομένης της κρυπτογράφησης δεδομένων και της ανίχνευσης σφαλμάτων και των αλγορίθμων διόρθωσης, όπως οι έλεγχοι ισοτιμίας και η δημιουργία κώδικα ελέγχου κυκλικού ελέγχου (CRC), οι πλήρεις adpers είναι ζωτικής σημασίας για την εκτέλεση βασικών εργασιών BIT.

Πάγκοι

Στους ψηφιακούς μετρητές, οι πλήρεις adpers είναι απαραίτητοι για την εφαρμογή τόσο των λειτουργιών αύξησης όσο και της μείωσης, ιδιαίτερα σε αρθρωτές και σύγχρονους μετρητές.Διαχειρίζονται με ακρίβεια τη μεταφορά και το δανεισμό για να εξασφαλίσουν ακριβή καταμέτρηση.

Πολυπλέκτες (MUX) και αποπολειπτικές (Demux)

Σε πολυπλέκτες και απομακρυσμένες εκκρίσεις, οι πλήρεις adders διαδραματίζουν κρίσιμο ρόλο στην επιλογή καναλιών και τη διανομή δεδομένων.Συμμετέχουν στη λογική που καθορίζει ποια κανάλια χρησιμοποιούνται για την είσοδο και την έξοδο δεδομένων, λαμβάνοντας αποφάσεις που βασίζονται σε σήματα λογικής ελέγχου.

Τεχνολογία μνήμης

Στη διεύθυνση μνήμης, οι πλήρεις πρόσθετες βοηθούν στη δημιουργία σημάτων διευθύνσεων για δυναμικά πρόσβαση σε τοποθεσίες μνήμης.Αυτό είναι ιδιαίτερα σημαντικό στη δυναμική μνήμη τυχαίας πρόσβασης (DRAM) και σε άλλα συστήματα αποθήκευσης, όπου οι πλήρεις προσθήκη υποστηρίζουν τους υπολογισμούς σύμπλεξης για την ενίσχυση της αποτελεσματικότητας της πρόσβασης στη μνήμη.

Αριθμητικές μονάδες λογικής (ALU)

Τέλος, ως θεμελιώδη συστατικά των αριθμητικών μονάδων λογικής σε μικροεπεξεργαστές και επεξεργαστές ψηφιακού σήματος, οι πλήρεις adpers είναι κρίσιμοι.Το ALU χειρίζεται όλες τις αριθμητικές και λογικές λειτουργίες, με πλήρη πρόσθετα να διασφαλίζουν ότι τα δεδομένα επεξεργάζονται τόσο γρήγορα όσο και με ακρίβεια.

Παραδείγματα πλήρους υλοποιήσεων αθροίσματος

Οι πλήρεις adders μπορούν να κατασκευαστούν χρησιμοποιώντας διάφορες λογικές πύλες και διαμορφώσεις.Εδώ, διερευνούμε τέσσερις διαφορετικές υλοποιήσεις, επισημαίνοντας τη ρύθμιση και τις επιχειρησιακές αποχρώσεις τους.

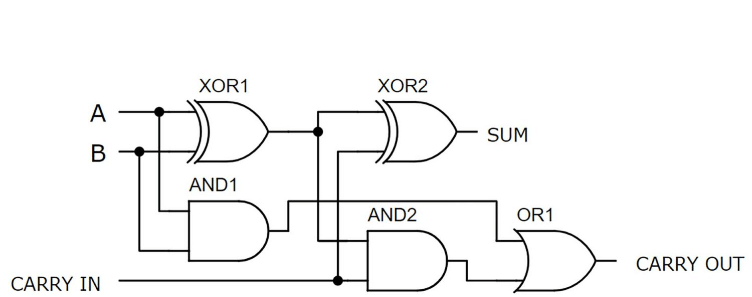
Ο πλήρης αθροιστής χτίστηκε με XOR και, και ή πύλες

Full Adder Built with XOR, AND, and OR Logic Gates

Εικόνα 6: Πλήρης αθροιστής που χτίστηκε με XOR και, και ή λογικές πύλες

Αυτό το παράδειγμα παρουσιάζει έναν πλήρη αθροιστή χτισμένο σε ένα breadboard χρησιμοποιώντας διακριτά τρανζίστορ.Η διαμόρφωση περιλαμβάνει πέντε λογικές πύλες: δύο πύλες XOR, δύο και πύλες, και μία ή πύλη, απαιτώντας συνολικά 21 τρανζίστορ.Οι εισόδους Α και Β συνδέονται με το επάνω αριστερό μέρος του breadboard, λαμβάνοντας μια τροφοδοσία +5V.Αυτές οι εισόδους ελέγχονται χρησιμοποιώντας δύο διακόπτες εναλλαγής.Δύο LED στο επάνω αριστερό μέρος υποδεικνύουν τις καταστάσεις των εισροών Α και Β, ενώ δύο LED στη δεξιά πλευρά εμφανίζουν τις εξόδους.Οι αντιστάσεις που χρησιμοποιούνται στο κύκλωμα είναι όλα 2,2k ohms.Όταν οι εισόδους Α και Β είναι ενεργοποιημένες και η μεταφορά είναι απενεργοποιημένη, η έξοδος δείχνει μια δυαδική τιμή 10, που αντιπροσωπεύει το άθροισμα 2 (1 + 1 + 0 = 10).Οι πύλες XOR, που χτίστηκαν με τα πρώτα 12 τρανζίστορ, χειρίζονται το κύριο άθροισμα, ενώ το κάτω μισό του breadboard περιέχει τις και και ή τις πύλες για λειτουργίες μεταφοράς, η καλωδίωση με χρωματική κωδικοποίηση ενισχύει τη σαφήνεια και την αντιμετώπιση προβλημάτων.

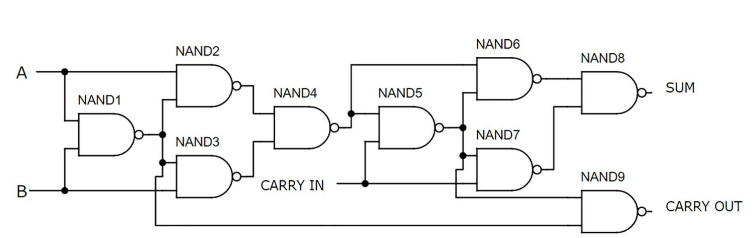
Πλήρης αθροιστής χρησιμοποιώντας τις πύλες Nand

Εικόνα 7: Πλήρης αθροιστής χρησιμοποιώντας πύλες NAND

Αυτός ο πλήρης αθροιστής χρησιμοποιεί εννέα πύλες Nand, με κάθε πύλη από δύο τρανζίστορ, συνολικά 18 τρανζίστορ.Αυτή η μέθοδος είναι ένας από τους απλούστερους και αποτελεσματικότερους τρόπους για την κατασκευή ενός πλήρους αθροιστή χρησιμοποιώντας διακριτά συστατικά.Όλες οι πύλες συναρμολογούνται στο πάνω μισό του breadboard, ενώ οι διακόπτες καταλαμβάνουν το κάτω μισό.Η λειτουργικότητα του κυκλώματος καταδεικνύεται με τις εισόδους Α και Β και την απενεργοποίηση, με αποτέλεσμα μια δυαδική τιμή εξόδου 10, ισοδύναμη με το δεκαδικό 2.

Πλήρης αθροιστής με Nor Gates

Εικόνα 8: Πλήρης αθροιστής με πύλες NOR

Κατασκευασμένο με εννέα ούτε πύλες, το καθένα που απαιτεί δύο τρανζίστορ, αυτή η ρύθμιση χρησιμοποιεί επίσης 18 τρανζίστορ συνολικά.Η οικοδόμηση ενός πλήρους αθροιστή με NOR Gates προσφέρει μια καλή εναλλακτική λύση, αλλά περιλαμβάνει πιο περίπλοκη καλωδίωση σε σύγκριση με τις πύλες NAND.Κάθε τρανζίστορ στο NOR Gates είναι γειωμένο, με τους συλλέκτες που συνδέονται με καλώδια πορτοκαλιού για να εξασφαλίσουν τακτοποιημένη και οργανωμένη καλωδίωση.Αυτή η διαμόρφωση εμφανίζεται με τις εισόδους Α και Β ενεργοποιημένες και η μεταφορά απενεργοποιημένη, οδηγώντας στις εξόδους όπου η μεταφορά είναι ενεργή και το άθροισμα είναι απενεργοποιημένο.

Σύναψη

Σε όλη αυτή την εξερεύνηση της τεχνολογίας ατόμων, από τα βασικά μισά προσανατολισμένα σε εξελιγμένα πλήρη σχέδια αθροιστών, είναι προφανές ότι αυτά τα εξαρτήματα είναι θεμελιώδη για την πρόοδο των ψηφιακών ηλεκτρονικών.Τα επιχειρησιακά χαρακτηριστικά και τα παραδείγματα εφαρμογής παρέχονται υπογραμμίζουν την ευελιξία και την αποτελεσματικότητα των προσθέτων σε διάφορες υπολογιστικές ρυθμίσεις.Με την εξέταση της δομής και της λειτουργίας των adpers, ιδιαίτερα μέσω των πινάκων αλήθειας και των χαρακτηριστικών εξισώσεων, κερδίζουμε πολύτιμες γνώσεις στις δυνατότητες και τους περιορισμούς τους.Αυτή η γνώση είναι καθοριστική για την προώθηση του σχεδιασμού πιο αποτελεσματικών και ταχύτερων υπολογιστικών συστημάτων.Τελικά, οι προσανατολισμοί όχι μόνο απλοποιούν πολύπλοκους δυαδικούς υπολογισμούς αλλά και επιτρέπουν τον πολλαπλασιασμό της τεχνολογίας σε περιοχές τόσο διαφορετικές όσο η επεξεργασία δεδομένων, η κατανομή της μνήμης και η επεξεργασία ψηφιακού σήματος.Καθώς εξελίσσεται η ψηφιακή τεχνολογία, η συνεχιζόμενη βελτίωση και η καινοτομία στο σχεδιασμό των ατόμων θα συνεχίσουν να αποτελούν ακρογωνιαίο λίθο στην ανάπτυξη πιο προηγμένων υπολογιστικών αρχιτεκτονικών, εξασφαλίζοντας ότι αυτά τα θεμελιώδη συστατικά παραμένουν στο επίκεντρο του σχεδιασμού και της εφαρμογής του ψηφιακού συστήματος.

Συχνές ερωτήσεις [FAQ]

1. Τι είναι ένα πλήρες κύκλωμα αθροιστή;

Ένας πλήρης αθροιστής είναι ένα ψηφιακό κύκλωμα που προσθέτει τρία δυαδικά bits για να παράγει ένα άθροισμα και μια έξοδο μεταφοράς.Έχει σχεδιαστεί για να χειρίζεται την προσθήκη τριών εισόδων: δύο σημαντικά bits και ένα bit μεταφοράς από μια προηγούμενη προσθήκη.Αυτό το επιτρέπει να χρησιμοποιείται σε διαδοχικά στάδια για να προσθέσει δυαδικούς αριθμούς πολλαπλών ψηφίων.

2. Πόσα και, ή XOR σε πλήρη αθροιστή;

Ένας τυπικός πλήρης αθροιστής περιέχει:

Δύο πύλες XOR για τη δημιουργία του αθροίσματος.

Δύο και πύλες για να συμβάλουν στον υπολογισμό της εκτέλεσης.

Μία ή πύλη για την ολοκλήρωση της εξόδου μεταφοράς.

3. Τι είναι η εισροή μεταφοράς σε πλήρη αθροιστή;

Η είσοδος μεταφοράς (CIN) σε ένα πλήρες αθροιστικό είναι το bit μεταφοράς από την προσθήκη των προηγούμενων χαμηλότερων σημαντικών δυαδικών ψηφίων σε δυαδική προσθήκη πολλαπλών ψηφίων.Επιτρέπει στον πλήρη αθροιστή να εξετάσει αυτή την προηγούμενη μεταφορά κατά τον υπολογισμό του τρέχοντος ποσού και της νέας μεταφοράς.

4. Γιατί να χρησιμοποιήσετε έναν πλήρη αθροιστή αντί για μισό αθροιστή;

Χρησιμοποιείται πλήρης αθροιστής αντί για μισό αθροιστή επειδή μπορεί να προσθέσει τρία bits (συμπεριλαμβανομένης της μεταφοράς από προηγούμενες προσθήκες), καθιστώντας το κατάλληλο για την αλυσίδα για να προσθέσετε αριθμούς πολλαπλών ψηφίων.Ένας μισός άνθρωπος μπορεί να προσθέσει μόνο δύο bits και δεν έχει πρόβλεψη για μια μεταφορά, η οποία περιορίζει τη χρήση του στις απλούστερες μορφές δυαδικής προσθήκης χωρίς διαδοχική διάδοση μεταφοράς.

Σχετικά με εμάς

ALLELCO LIMITED

Το Allelco είναι ένα διεθνώς διάσημο one-stop Διανομέας υπηρεσιών προμηθειών υβριδικών ηλεκτρονικών εξαρτημάτων, που δεσμεύεται να παρέχει ολοκληρωμένες υπηρεσίες προμηθειών και αλυσίδας εφοδιασμού για τις παγκόσμιες ηλεκτρονικές βιομηχανίες κατασκευής και διανομής, συμπεριλαμβανομένων των παγκόσμιων 500 εργοστασίων OEM και των ανεξάρτητων μεσίων.
Διαβάστε περισσότερα